a) e b) Sulla boccia è esercitata una forza normale di modulo
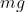
, quindi l'attrito è
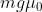
. Abbiamo allora che
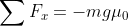
, da cui
=v_0-g\mu_0t)
finchè siamo in regime di scivolamento. Contemporaneamente, l'attrito esercita un momento torcente
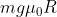
, perciò, ricordando che il momento d'inerzia di una sfera piena è
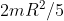
, vale
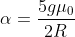
, da cui
=-\omega_0+\frac{5g\mu_0}{2R}t)
. Il rotolamento puro si ottiene quando
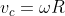
, dunque scriviamo
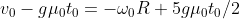
, da cui
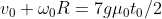
e
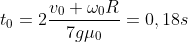
. Quindi
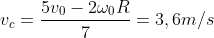
.
c) La boccia si arresta quando la velocità
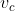
e
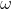
sono nulle. Ricorrendo alle precedenti equazioni,
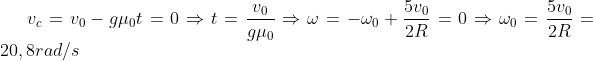
.