Serie di Taylor
Serie di Taylor
Buonasera... Leggendo sul sillabo ufficiale è richiesto l'uso dell'approssimazione mediante serie di Taylor. Ho cercato su internet, ho letto diversi articoli tuttavia ho trovato troppo formalismo e pochi esempi. Qualcuno mi spiega un'esempio di approssimazione con serie di Taylor applicato in un problema delle olifis?
Re: Serie di Taylor
Ad esempio nel problema 1 della prova di Febbraio 2018 ti suggeriscono che ^\alpha \approx 1 + \alpha x) per
per 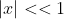 . Nelle fasi successive non ci sarebbe stato questo suggerimento e uno si sarebbe dovuto ricordare questa formula, o l'avrebbe dovuta ricavare con l'approssimazione di Taylor. Infatti se
. Nelle fasi successive non ci sarebbe stato questo suggerimento e uno si sarebbe dovuto ricordare questa formula, o l'avrebbe dovuta ricavare con l'approssimazione di Taylor. Infatti se  = (1+x)^\alpha) ,
,  \approx f(0) + f'(0) x = 1 + \alpha x) . Questa formula e' cosi' facile che uno puo' anche ricordarsela, ma a volte (piu' spesso di quanto immagineresti) servono anche i termini successivi,
. Questa formula e' cosi' facile che uno puo' anche ricordarsela, ma a volte (piu' spesso di quanto immagineresti) servono anche i termini successivi,  \approx 1 + \alpha x + \frac{1}{2} \alpha (\alpha - 1) x^2 + ...) . Altre volte serve approssimare formule trigonometriche per angoli piccoli (e non solo
. Altre volte serve approssimare formule trigonometriche per angoli piccoli (e non solo 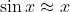 ).
).
Insomma, fidati che l'analisi serve...
Insomma, fidati che l'analisi serve...
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
Re: Serie di Taylor
Grazie Pigkappa. Nell'esempio che hai fatto tu con ) hai utilizzato quindi MacLaurin?
hai utilizzato quindi MacLaurin?
Re: Serie di Taylor
Sì, ma sinceramente ho appena scoperto che la serie di Taylor si chiama serie di Maclaurin se è centrata in 0. Tanto vale ricordarsi la formula intorno a un punto generico e chiamarla sempre e solo serie di Taylor...
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
Re: Serie di Taylor
In base a cosa scelgo il punto?
