carica dentro una sfera cava conduttrice (senza carica)
carica dentro una sfera cava conduttrice (senza carica)
finché la carica si trova al centro i problemi non si pongono ma se la carica dentro la sfera conduttrice cava viene spostata ho letto che il campo fuori dalla sfera dovrebbe essere ancora simmetrico, o in altre parole il guscio sferico è una sorta di raddrizzatore , sinceramente non ne sono troppo convinto, cioè se te muovi la carica all'interno del guscio al di fuori il campo elettrico rimane invariato?
Se Dio esiste, è un grande matematico.(Paul Dirac)
- OrsoBruno96
- Messaggi: 103
- Iscritto il: 31 mag 2013, 16:17
- Località: Udine
Re: carica dentro una sfera cava conduttrice (senza carica)
Si, esatto. Stiamo comunque parlando di elettrostatica, quindi devi considerare la carica ferma in un punto diverso dal centro del guscio
Fatti un disegno bello grande e applica il teorema di Gauss.
Il guscio ha raggi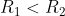 . Applica Gauss ad una superficie sferica di raggio
. Applica Gauss ad una superficie sferica di raggio 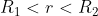 , ricordando come si comportano i conduttori.
, ricordando come si comportano i conduttori.
Una volta fatto questo, applica Gauss fuori dal guscio e cerca di convincerti che funziona quello che hai detto
Fatti un disegno bello grande e applica il teorema di Gauss.
Il guscio ha raggi
Una volta fatto questo, applica Gauss fuori dal guscio e cerca di convincerti che funziona quello che hai detto
"La fisica non è complicata, sono i fisici ad esserlo."
"Sai cosa vuol dire ? Vuol dire chiudi la porta che c'è il condizionatore acceso."
? Vuol dire chiudi la porta che c'è il condizionatore acceso."
"Sai cosa vuol dire
Re: carica dentro una sfera cava conduttrice (senza carica)
Aggiungo la mia interpretazione su questo fenomeno. Secondo me non c'e' un modo intuitivo per capire il risultato descritto da wotzu, che e' corretto e spesso citato come ovvio, senza tirare in ballo un po' di matematica avanzata.
E' utile sapere che c'e' un teorema che dice che se c'e' una regione dello spazio senza cariche per la quale si conosce il potenziale su tutte le superfici che la delimitano, allora il potenziale e' univocamente determinato in tutta quella regione (e si puo' anche calcolare - ma spesso questo richiede conti complicati). Questo teorema fa parte della teoria sulla soluzione dell'equazione di Laplace, che se volete potete cercarvi su Wikipedia, ma va oltre quel che di solito si studia prima dell'universita'. E' molto utile ricordarsi questo fatto.
Una volta che sappiamo che esiste questo teorema, quel risultato diventa naturale. Ovunque sia la carica nella sfera, sappiamo che il conduttore sferico deve essere tutto allo stesso potenziale per definizione. Quindi il potenziale sulla superficie esterna del conduttore e' lo stesso in ogni punto. La regione dello spazio da considerare e' delimitata da tale superficie esterna e dalla superficie all'infinito (in cui il potenziale e' 0). Il potenziale sulle superfici che delimitano questa regione ha simmetria sferica rispetto al centro della sfera; percio' il potenziale e il campo elettrico in ogni punto dovranno avere simmetria sferica. Una volta dimostrato cio', si puo' usare la legge di Gauss per calcolarli.
E' utile sapere che c'e' un teorema che dice che se c'e' una regione dello spazio senza cariche per la quale si conosce il potenziale su tutte le superfici che la delimitano, allora il potenziale e' univocamente determinato in tutta quella regione (e si puo' anche calcolare - ma spesso questo richiede conti complicati). Questo teorema fa parte della teoria sulla soluzione dell'equazione di Laplace, che se volete potete cercarvi su Wikipedia, ma va oltre quel che di solito si studia prima dell'universita'. E' molto utile ricordarsi questo fatto.
Una volta che sappiamo che esiste questo teorema, quel risultato diventa naturale. Ovunque sia la carica nella sfera, sappiamo che il conduttore sferico deve essere tutto allo stesso potenziale per definizione. Quindi il potenziale sulla superficie esterna del conduttore e' lo stesso in ogni punto. La regione dello spazio da considerare e' delimitata da tale superficie esterna e dalla superficie all'infinito (in cui il potenziale e' 0). Il potenziale sulle superfici che delimitano questa regione ha simmetria sferica rispetto al centro della sfera; percio' il potenziale e il campo elettrico in ogni punto dovranno avere simmetria sferica. Una volta dimostrato cio', si puo' usare la legge di Gauss per calcolarli.
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
