Qualcuno può gentilmente illustrare in cosa consiste matematicamente il metodo dei minimi quadrati? Quando si può utilizzare?
Grazie, in anticipo.
Metodo dei minimi quadrati
Re: Metodo dei minimi quadrati
Supponi di avere 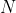 coppie di dati
coppie di dati ,\ (x_2, y_2),\ \dots,\ (x_n, y_n)) e di voler cercare la miglior retta
e di voler cercare la miglior retta  = A x + B) per fittare questi dati.
per fittare questi dati.
Definiamo:
 = \sum_{i=1}^N{(y(x_i) - y_i)^2} = \sum_{i=1}^N{(Ax_i +B - y_i)^2})
Cerca di capire graficamente cosa è C; è la somma dei quadrati delle lunghezze in verde:

Il metodo dei minimi quadrati consiste nel calcolare i migliori A e B minimizzando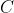 .
.
Per calcolare e
e  esplicitamente, si impone che
esplicitamente, si impone che 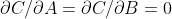 , ma probabilmente non sai cosa vuol dire. Quando in una prova sperimentale delle olimpiadi devi trovare la miglior retta con
, ma probabilmente non sai cosa vuol dire. Quando in una prova sperimentale delle olimpiadi devi trovare la miglior retta con  e
e  entrambi non nulli, conviene che lo fai per via grafica, disegnando i punti e trovando ad occhio la retta migliore.
entrambi non nulli, conviene che lo fai per via grafica, disegnando i punti e trovando ad occhio la retta migliore.
Se sai già che è zero, e quindi la retta passa per l'origine, la funzione
è zero, e quindi la retta passa per l'origine, la funzione ) è una parabola; quindi il minimo è nel vertice e lo sai calcolare.
è una parabola; quindi il minimo è nel vertice e lo sai calcolare.
Definiamo:
Cerca di capire graficamente cosa è C; è la somma dei quadrati delle lunghezze in verde:

Il metodo dei minimi quadrati consiste nel calcolare i migliori A e B minimizzando
Per calcolare
Se sai già che
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
-
Eagle
Re: Metodo dei minimi quadrati
Allora, vediamo un po' cosa ho capito.
=(y(x_i)-y_i)^2)
è la differenza tra il valore teorico, che esce fuori dalla miglior retta, e il valore reale, che ho trovato nell'esperimento: diciamo, quindi, uno scarto quadratico.
Essendo lo scopo dei minimi quadrati calcolare i migliori e
e  minimizzando
minimizzando 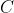 , si fanno le derivate parziali di
, si fanno le derivate parziali di 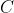 rispetto
rispetto  e poi di
e poi di 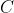 rispetto a
rispetto a  , uguagliandole a 0.
, uguagliandole a 0.
C'ho messo un po' a capire quello che hai scritto (e non so se ho capito tutto ), comunque derivare e uguagliare a 0 ti permette di trovare dove la funzione ha un minimo (es. vertice della parabola).
), comunque derivare e uguagliare a 0 ti permette di trovare dove la funzione ha un minimo (es. vertice della parabola).
Poiché consideri nell'equazione della retta due incognite, il coefficiente angolare e
il coefficiente angolare e  l'intercetta, derivi
l'intercetta, derivi 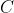 prima rispetto a
prima rispetto a  (considerando costante
(considerando costante  ) e poi rispetto a
) e poi rispetto a  (considerando costante
(considerando costante  ), uguagliando a 0, in modo da trovarti gli
), uguagliando a 0, in modo da trovarti gli  e
e  migliori. Non so se è giusto, comunque correggimi se ho scritto eresie.
migliori. Non so se è giusto, comunque correggimi se ho scritto eresie.
è la differenza tra il valore teorico, che esce fuori dalla miglior retta, e il valore reale, che ho trovato nell'esperimento: diciamo, quindi, uno scarto quadratico.
Essendo lo scopo dei minimi quadrati calcolare i migliori
C'ho messo un po' a capire quello che hai scritto (e non so se ho capito tutto
Poiché consideri nell'equazione della retta due incognite,
Re: Metodo dei minimi quadrati
Di solito alcune calcolatrici con funzioni statistiche una volta inseritiPigkappa ha scritto:Quando in una prova sperimentale delle olimpiadi devi trovare la miglior retta cone
entrambi non nulli, conviene che lo fai per via grafica, disegnando i punti e trovando ad occhio la retta migliore.
Re: Metodo dei minimi quadrati
Penso che vada bene; in una soluzione lo facevano anche loro, mi pare, e non ci vedo nulla di male. E' un metodo furbo per risparmiare tempo e conviene imparare a fare un po' di queste cose con la calcolatrice.fisicorel ha scritto:Di solito alcune calcolatrici con funzioni statistiche una volta inseritie
danno i coefficienti
e
.Scrivere sulla relazione della prova sperimentale che la retta migliore l'ho trovata con la calcolatrice senza fare il grafico(che occupa tanto tempo)è grave e da evitare?
E' giusto, però non pensare che la cosa si possa generalizzare troppo facilmente e che il massimo o minimo di qualunque funzione in 2 (o più) variabili definita su qualunque insieme si trovi imponendo che le derivate parziali si annullino. Mentre per funzioni di una variabile questa cosa funziona abbastanza bene (almeno finchè la funzione è derivabile e il dominio è un intervallo e ci si ricorda di controllare cosa fa la funzione nei due punti all'estremo dell'intervallo), con più di una variabile la situazione è un po' più delicata (perchè i punti "all'estremo dell'intervallo" non sono 2 ma sono infiniti).Eagle ha scritto:Essendo lo scopo dei minimi quadrati calcolare i migliorie
minimizzando
, si fanno le derivate parziali di
rispetto
e poi di
rispetto a
, uguagliandole a 0.
C'ho messo un po' a capire quello che hai scritto (e non so se ho capito tutto), comunque derivare e uguagliare a 0 ti permette di trovare dove la funzione ha un minimo (es. vertice della parabola).
Se vuoi scoprire i dettagli cerca i moltiplicatori di Lagrange...
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
-
Eagle
Re: Metodo dei minimi quadrati
Grazie mille, Pigkappa. Comunque ho leggiucchiato qualcosa sui moltiplicatori di Lagrange, ma penso che sia ancora presto (  )
)
