4.
La distanza
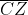
cambia con accelerazione
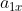
, pertanto
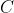
si sovrappone a
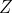
in un tempo dato da
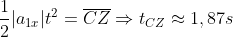
.
Similmente si ricava il tempo di caduta della massa
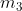
: la distanza iniziale di
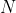
dal suolo è data da
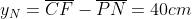
poichè i blocchi sono cubici, dunque
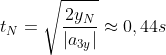
.
Infine, la distanza
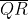
varia con accelerazione
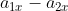
, quindi
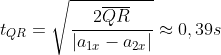
.
Poichè
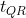
è il tempo minore, il moto del sistema termina quando il blocco
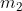
urta la carrucola.
5.
Se non c'è la guida verticale, le uniche forze agenti su
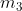
sono il suo peso e la tensione

, inizialmente entrambe verticali, quindi:
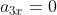
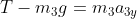
La tensione agisce come prima su
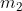
:

Inoltre valgono ancora la condizione
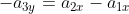
dovuta alla geometria del sistema e la conservazione della quantità di moto lungo

:
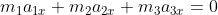
.
Risolvendo il sistema ottengo:
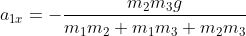

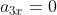
 m_3 g}{m_1 m_2+ m_1 m_3 + m_2 m_3})
6. Il moto del sistema prosegue con la massa
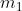
che si sposta verso sinistra, la massa
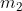
che si muove a destra e la massa
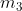
che cade oscillando a destra e a sinistra. Le accelerazioni trovate al punto precedente non sono costanti perchè appena i due blocchi si muovono la fune non si trova più ad essere verticale, e quindi
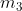
assume anche un'accelerazione orizzontale variabile. Poichè continuano a non agire forze esterne orizzontali sul sistema, la sua quantità di moto non cambia e perciò variano anche le accelerazioni dei blocchi.
7. Le forze orizzontali agenti inizialmente sul blocco più grande sono la forza elastica dovuta alla molla e una forza di reazione in modulo pari alla tensione che la carrucola esercita, tramite la fune inestensibile, sul blocco più piccolo. La prima ha modulo
)
e punta a destra poichè la molla è compressa. La seconda si può ottenere dalle equazioni del punto 1. poichè la situazione è analoga (
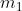
immobile,
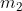
ed
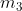
soggetti alla gravità). Pertanto
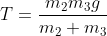
.
Uguagliando le forze si ricava
(l_0-\overline{R_1 D_1})} \approx 32,7 N/m)
.
Inoltre, sapendo che neanche il pistone si muove, è possibile ricavare il valore iniziale della pressione del gas in esso contenuto, che sarà utile più avanti:
 \Rightarrow P_1 \approx 101,5 kPa)
.
8. Siano
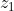
e
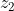
rispettivamente le distanze iniziale e finale del pistone dal fondo del recipiente (parete di sinistra). Sappiamo che
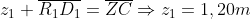
, mentre
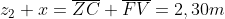
, dove

è la lunghezza finale della molla. Detta
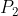
la pressione finale del gas, vale per l'equilibrio:
)
Poichè le pareti di contenitore e pistone sono diatermiche, la temperatura finale del gas sarà pari alla temperatura ambiente
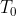
che era anche la sua temperatura iniziale, perciò, supponendo valida l'equazione di stato dei gas perfetti (non mi sembra che il testo dica se il gas è ideale), vale
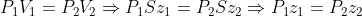
. Risolvendo queste equazioni trovo
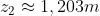
, da cui
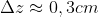
, un valore che mi sembra molto piccolo, ma sinceramente sono morto di LaTeX e non credo che riuscirei a ricontrollare i conti per bene adesso

. Aspetto correzioni.
), mentre tu hai usato
. Quale delle due è corretta?
. In una gara andrebbe bene oppure si tratta di un metodo non olimpico?