Hint. Dove è massima la differenza fra questi momenti (punto P) la ciminiera si spezza
219. La ciminiera si spezza
219. La ciminiera si spezza
Un'alta e affusolata ciminiera di mattoni di lunghezza L e massa m viene allontanata dalla sua posizione di equilibrio verticale da una scossa tellurica e ruota di un angolo) rispetto alla verticale, avendo un momento di inerzia
rispetto alla verticale, avendo un momento di inerzia mL^2) rispetto alla base B, finchè si spezza in un punto P distante x dalla base B. Si determini x assumendo che la parte (L-x) della ciminiera sopra P sia soggetta ad un momento generato dal suo centro di massa più forte rispetto a quello generato dalla parte x sotto P che tende invece a farla ruotare all'accelerazione angolare prevista dall'equazione del moto.
rispetto alla base B, finchè si spezza in un punto P distante x dalla base B. Si determini x assumendo che la parte (L-x) della ciminiera sopra P sia soggetta ad un momento generato dal suo centro di massa più forte rispetto a quello generato dalla parte x sotto P che tende invece a farla ruotare all'accelerazione angolare prevista dall'equazione del moto.
Hint. Dove è massima la differenza fra questi momenti (punto P) la ciminiera si spezza
Hint. Dove è massima la differenza fra questi momenti (punto P) la ciminiera si spezza
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 219. La ciminiera si spezza
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 219. La ciminiera si spezza
Il tuo x attualmente non è corretto. Magari riguarda i conti mi sembra che sei sulla giusta via. Se ci pensi è improbabile che si spezzi solo l'utimo terzo 
Re: 219. La ciminiera si spezza
Da quel che ricordo quel risultato non e' corretto ma assomiglia a quello giusto. Se posti direttamente il procedimento invece di fare il giochino "dimmi se questo e' giusto e poi posto" possiamo risparmiare un paio di giorni di interazioni a vuoto
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 219. La ciminiera si spezza
Ok allora io ho ragionato così:
Per prima cosa ricavo l'accelerazione angolare della ciminiera in funzione di , e trovo, essendo
, e trovo, essendo 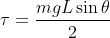 e
e 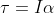 :
:
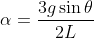 .
.
Ora guardo alla prima metà della ciminiera (quella di lunghezza ). Il suo momento d'inerzia rispetto alla base vale
). Il suo momento d'inerzia rispetto alla base vale 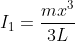 , pertanto su di esso deve agire un momento torcente totale pari a
, pertanto su di esso deve agire un momento torcente totale pari a 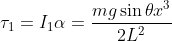 . Il momento agente su questa parte di ciminiera dovuto alla gravità vale
. Il momento agente su questa parte di ciminiera dovuto alla gravità vale 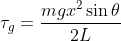 , quindi agisce anche un momento addizionale di modulo
, quindi agisce anche un momento addizionale di modulo }{2L^2}) , che si oppone al moto. Lo stesso momento torcente agisce, in senso contrario, sulla seconda parte di ciminiera: ho fatto i conti con la parte lunga
, che si oppone al moto. Lo stesso momento torcente agisce, in senso contrario, sulla seconda parte di ciminiera: ho fatto i conti con la parte lunga  per semplicità. A questo punto ho ritenuto che il punto di rottura più probabile fosse quello in cui il momento torcente addizionale è massimo, cioè in
per semplicità. A questo punto ho ritenuto che il punto di rottura più probabile fosse quello in cui il momento torcente addizionale è massimo, cioè in 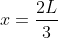 . Però anche a me sembra strano che la ciminiera si rompa così in alto, e in effetti bosone ha detto che il risultato è sbagliato. Non riesco a capire se ho fatto qualche errore nel procedimento o se devo tentare un approccio del tutto diverso...
. Però anche a me sembra strano che la ciminiera si rompa così in alto, e in effetti bosone ha detto che il risultato è sbagliato. Non riesco a capire se ho fatto qualche errore nel procedimento o se devo tentare un approccio del tutto diverso...
Per prima cosa ricavo l'accelerazione angolare della ciminiera in funzione di
Ora guardo alla prima metà della ciminiera (quella di lunghezza
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 219. La ciminiera si spezza
Lascio controllare a bosone 
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
Re: 219. La ciminiera si spezza
Intanto credo che ci sia una differenza con la soluzione nell'acc. angolare. Dovrebbe esserci un coseno se indichiamo con  l'angolo formato dalla ciminiera con l'orizzontale ( ma penso che tu abbia indicato il suo complementare). Questo comunque è poco rilevante. Poi analizza (L-x), non x. Calcola due momenti di (L-x): 1) rispetto alla base per quanto riguarda il suo peso (che puoi esprimere poi per mezzo dell'acc.angolare) 2) con la formula del moto mutatis mutandis cioè riferendoci a (L-x) (e non ad L) ancora per mezzo dell'acc. angolare. Trova il max (vedi hint nel testo) della differenza dei loro moduli e il gioco dovrebbe essere fatto. Il risultato è molto simile al tuo ma....
l'angolo formato dalla ciminiera con l'orizzontale ( ma penso che tu abbia indicato il suo complementare). Questo comunque è poco rilevante. Poi analizza (L-x), non x. Calcola due momenti di (L-x): 1) rispetto alla base per quanto riguarda il suo peso (che puoi esprimere poi per mezzo dell'acc.angolare) 2) con la formula del moto mutatis mutandis cioè riferendoci a (L-x) (e non ad L) ancora per mezzo dell'acc. angolare. Trova il max (vedi hint nel testo) della differenza dei loro moduli e il gioco dovrebbe essere fatto. Il risultato è molto simile al tuo ma.... 
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 219. La ciminiera si spezza
Per quanto riguarda l'angolo, io leggo nel testo del problema che  viene misurato rispetto alla verticale, e per questo ho usato
viene misurato rispetto alla verticale, e per questo ho usato 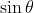 . Comunque, penso di aver capito dove sbagliavo. Prendendo come polo dei momenti il punto
. Comunque, penso di aver capito dove sbagliavo. Prendendo come polo dei momenti il punto 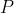 e non la base
e non la base  della ciminiera, allora il momento di inerzia della parte
della ciminiera, allora il momento di inerzia della parte ) vale
vale ^3}{3L}) , quindi il momento torcente totale è
, quindi il momento torcente totale è ^3}{3L}) . Il momento torcente dovuto alla gravità risulta
. Il momento torcente dovuto alla gravità risulta ^2}{2L}=\frac{m\alpha(L-x)^2}{3}) , quindi la differenza vale
, quindi la differenza vale ^2}{3L}) , che è massimo in
, che è massimo in 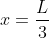 , un valore di
, un valore di  che mi sembra molto più plausibile. In effetti non aveva molto senso considerare i momenti rispetto a
che mi sembra molto più plausibile. In effetti non aveva molto senso considerare i momenti rispetto a  , dato che la rottura avviene in
, dato che la rottura avviene in 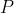 . Chiedo conferma del risultato.
. Chiedo conferma del risultato.
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 219. La ciminiera si spezza
Si, ci siamo 
 Vai con il 220!
Vai con il 220!
