Bosona ma esiste un modo elementare (o comunque più fisico) di mostrare che
202. Corsa sul ghiaccio
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 202. Corsa sul ghiaccio
Io ho inteso "traiettoria ottimale" come quella che permette di cambiare velocità e direzione nel minor tempo possibile, cioè 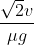 . Osservo che se la forza di attrito è sempre rivolta verso sud-est, cioè
. Osservo che se la forza di attrito è sempre rivolta verso sud-est, cioè 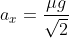 e
e 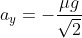 , allora la condizione è soddisfatta, poichè integrando ottengo:
, allora la condizione è soddisfatta, poichè integrando ottengo:
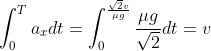
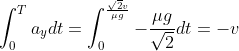
Quindi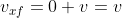 e
e 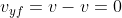 , che è quello che cerchiamo.
, che è quello che cerchiamo.
Per ottenere la traiettoria ricavo prima le due leggi orarie integrando le velocità:
=v_{xi}t+\frac{a_x t^2}{2}=0+\frac{\mu g t^2}{2\sqrt{2}})
=v_{yi}t+\frac{a_y t^2}{2}= vt-\frac{\mu g t^2}{2\sqrt{2}})
A questo punto ricavo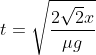 dalla prima e lo inserisco nella seconda, ottenendo:
dalla prima e lo inserisco nella seconda, ottenendo:
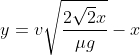 , equazione che descrive la traiettoria.
, equazione che descrive la traiettoria.
Poi se vuoi posso fare qualche altro passaggio e arrivare alla forma implicita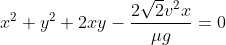 , che descrive una conica con gli assi di simmetria non paralleli agli assi cartesiani, ma non penso di poter andare oltre.
, che descrive una conica con gli assi di simmetria non paralleli agli assi cartesiani, ma non penso di poter andare oltre.
Quindi
Per ottenere la traiettoria ricavo prima le due leggi orarie integrando le velocità:
A questo punto ricavo
Poi se vuoi posso fare qualche altro passaggio e arrivare alla forma implicita
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
-
east_beast
- Messaggi: 136
- Iscritto il: 2 mar 2020, 16:58
Re: 202. Corsa sul ghiaccio
Se il vettore accelerazione è costante e c'è una velocità iniziale non nulla e non parallela ad  la conica è una parabola con asse di simmetria la direzione del vettore accelerazione (analogia con il moto parabolico) giusto?
la conica è una parabola con asse di simmetria la direzione del vettore accelerazione (analogia con il moto parabolico) giusto?
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 202. Corsa sul ghiaccio
Ora che mi ci fai pensare, e dopo aver frettolosamente controllato con Geogebra, penso che sia proprio così...
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 202. Corsa sul ghiaccio
Nel grafico della velocita', dovete andare daeast_beast ha scritto: ↑30 apr 2020, 17:55Bosona ma esiste un modo elementare (o comunque più fisico) di mostrare che?
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
-
east_beast
- Messaggi: 136
- Iscritto il: 2 mar 2020, 16:58
Re: 202. Corsa sul ghiaccio
Non ci avevo proprio pensato, che ottuso
Re: 202. Corsa sul ghiaccio
Comunque questa situazione e' davvero realistica? Il pattinatore puo' dirigere la forza di attrito nella direzione che vuole per ottenere questo cambio di direzione? Non so la risposta ma sembra interessante.
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
-
Luca Milanese
- Messaggi: 452
- Iscritto il: 13 giu 2019, 10:05
- Località: Terracina
Re: 202. Corsa sul ghiaccio
Ah mannaggia a me che cerco sempre di complicarmi la vita...
@Pigkappa il testo non mi sembra parlare di un pattinatore, ma di un ragazzo che corre con delle scarpe, quindi probabilmente l'attrito in questione è quello statico, che magari è più facile da direzionare (anche perchè per quanto ne so quello dinamico è invece sempre opposto al movimento).
@Pigkappa il testo non mi sembra parlare di un pattinatore, ma di un ragazzo che corre con delle scarpe, quindi probabilmente l'attrito in questione è quello statico, che magari è più facile da direzionare (anche perchè per quanto ne so quello dinamico è invece sempre opposto al movimento).
Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems
Re: 202. Corsa sul ghiaccio
Ho letto campo gelato e mi sono immaginato un pattinatore  infatti mi stavo chiedendo come avrebbe fatto a orientare l'attrito nella direzione che voleva.
infatti mi stavo chiedendo come avrebbe fatto a orientare l'attrito nella direzione che voleva.
"Per un laser, si passa da temperature positive a temperature negative non passando attraverso 0 K, ma passando attraverso l'infinito!" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
"Perché dovremmo pagare uno scienziato quando facciamo le migliori scarpe del mondo?" (cit.)
Re: 202. Corsa sul ghiaccio
Allora siamo arrivati alla conclusione dopo un dibattito approfondito e concitato come si conviene nei problemi davvero intriganti. In realtà il metodo più semplice era, come avevo suggerito a east beast, di mettersi nel sistema) con il primo asse verso Est e il secondo verso Nord. Inizialmente siamo in A=(0,v) e alla fine siamo in B(v,0) - come mi pare abbia inteso Pigkappa. Ora il secondo estremo del vettore velocità
con il primo asse verso Est e il secondo verso Nord. Inizialmente siamo in A=(0,v) e alla fine siamo in B(v,0) - come mi pare abbia inteso Pigkappa. Ora il secondo estremo del vettore velocità  percorre la diagonale del quadrato di lato v, cioè
percorre la diagonale del quadrato di lato v, cioè 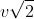 , nel tempo
, nel tempo 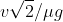 e quindi alla velocità costante
e quindi alla velocità costante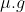 . E' facile allora calcolare le componenti di
. E' facile allora calcolare le componenti di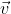 cioè
cioè , v_y(t)) che poi sono
che poi sono) e risalire a x e y e quindi all'equazione della conica come ha fatto Luca.
e risalire a x e y e quindi all'equazione della conica come ha fatto Luca.
Difficile assegnare il 203 perchè per esempio la parabola l'ha riconosciuta east beast. A scuola non si fanno queste cose. Personalmente ero andato sul web a farmi una cultura sulla classificazione delle coniche per stabilire che, avendo due intersezioni coincidenti con la retta all'infinito, era una parabola. In conclusione tuttavia, considerata anche la risposta 1),ritengo che abbia meritato il 203 Luca Milanese!

Difficile assegnare il 203 perchè per esempio la parabola l'ha riconosciuta east beast. A scuola non si fanno queste cose. Personalmente ero andato sul web a farmi una cultura sulla classificazione delle coniche per stabilire che, avendo due intersezioni coincidenti con la retta all'infinito, era una parabola. In conclusione tuttavia, considerata anche la risposta 1),ritengo che abbia meritato il 203 Luca Milanese!
