Mi è venuta in mente una soluzione bruttissima, ma mi pare funzionare:
Per quanto scritto sopra devo avere:
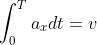
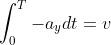
Ora applico
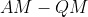
alle medie integrali di
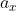
e
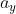
:
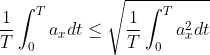
^2 dt})
Elevando al quadrato e moltiplicando per

ottengo:
^2 \leq \int_0^T a_x^2 dt)
^2 \leq \int_0^T (-a_y)^2 dt)
Infine, sommando membro a membro:
^2 +\bigg(\int_0^T -a_y dt \bigg)^2 \Bigg ] \leq \int_0^T (a_x^2+a_y^2) dt)
 \leq \int_0^T (\mu g)^2 dt \Rightarrow \frac{2v^2}{T} \leq (\mu g)^2 T \Rightarrow T \geq \frac{\sqrt{2}v}{\mu g})
.
Quanto poi alla traiettoria, penso che basti dire che, poichè con le leggi orarie scritte sopra si ottiene proprio
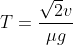
, allora esse (e quindi la traiettoria che ne deriva) vanno bene. In realtà penso che siano anche le uniche possibili, perchè, almeno nel caso discreto, l'uguaglianza in
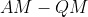
implica che tutti gli elementi di cui si fa la media siano uguali, e penso che lo stesso si possa dire nel caso continuo, dove quindi significherebbe che
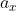
e
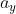
sono costanti.
Ora però spero che esista una soluzione più semplice che non ho trovato....