Si abbia un piano inclinato di un angolo α rispetto all’orizzontale sul quale è appoggiata e
tenuta ferma una sfera piena di raggio R. Sia A il punto della sfera che è in contatto con il
piano inclinato. In un certo istante la sfera viene lasciata libera di muoversi ed essa,
compreso il punto A, comincia a rotolare (senza strisciare) lungo il piano inclinato. Dopo
quanto tempo la velocità del punto A ha direzione orizzontale per la prima volta?
Moto di rotolamento
Re: Moto di rotolamento
Ho provato a farlo oggi e mi torna come te soltanto che anzichè alfa al numeratore ho ottenuto pigreco-2alfa 
Re: Moto di rotolamento
sono io che ho fatto male i conti... rimedio subito (e poi posto la soluzione) 
Re: Moto di rotolamento
Supponiamo che la velocità di A sia orizzontale dopo che A ha spazzato un angolo  . Si deve avere
. Si deve avere ) e siccome la sfera rotola senza strisciare (
e siccome la sfera rotola senza strisciare (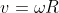 ),
),  => \theta = \pi -2\alpha) .
.
Si ha da cui
da cui 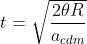 .
.
}{5g\sin\alpha }})

Si ha
Re: Moto di rotolamento
Bravo lance bella soluzione 

Propongo una variante di come si può trovare l'angolo .
.
La sfera quando rotola sta ruotando istantaneamente intorno al punto di contatto. Questo significa che la velocità istantanea di ogni punto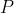 della sfera è perpendicolare alla congiungente di
della sfera è perpendicolare alla congiungente di 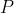 e il punto di contatto. Di conseguenza il punto con velocità orizzontale avrà la congiungente con il punto di contatto verticale, cioè sarà "sopra" di esso. Mi basta quindi calcolare l'angolo tra il punto di contatto e il punto di intersezione tra la sfera e la retta verticale passante per il punto di contatto.
e il punto di contatto. Di conseguenza il punto con velocità orizzontale avrà la congiungente con il punto di contatto verticale, cioè sarà "sopra" di esso. Mi basta quindi calcolare l'angolo tra il punto di contatto e il punto di intersezione tra la sfera e la retta verticale passante per il punto di contatto.
Si forma un triangolo isoscele con angolo alla base .
.
Quindi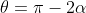


Spero si capisca, lo so che mi esprimo da cani
Propongo una variante di come si può trovare l'angolo
La sfera quando rotola sta ruotando istantaneamente intorno al punto di contatto. Questo significa che la velocità istantanea di ogni punto
Si forma un triangolo isoscele con angolo alla base
Quindi
Spero si capisca, lo so che mi esprimo da cani
Sapere aude 
