124. Pila di mattoni
124. Pila di mattoni
a) Si sovrappongono N mattoni di lunghezza l= 20 cm. Di quanto può sporgere al massimo la pila?
b) Stimare quanti mattoni sono necessari per far sporgere la pila di 1 km.
b) Stimare quanti mattoni sono necessari per far sporgere la pila di 1 km.
Re: 124. Pila di mattoni
Il CM degli N-! mattoni sopra il primo deve essere al massimo a 10 cm dal CM del primo messo a 0. Come CM abbiamo (N/2)x che dovrebbe essere moltiplicato e diviso per (N-1)=10 e x distanza fra i CM consecutivi. Da cui x=20/N come distanza fra CM di un mattone e del successivo. La sporgenza è l'ascissa dell'N-1mo CM cioè
A) (N-1)(20/N)
B) (N-1)(20/N)= 100000 è impossibile perchè al crescere di N (basta provare) la sporgenza tende a 20 ovvero non può superare secondo me la lunghezza del mattone.


A) (N-1)(20/N)
B) (N-1)(20/N)= 100000 è impossibile perchè al crescere di N (basta provare) la sporgenza tende a 20 ovvero non può superare secondo me la lunghezza del mattone.
Re: 124. Pila di mattoni
Se hai abbastanza mattoni puoi far sporgere la pila di quanto vuoi 
Re: 124. Pila di mattoni
Secondo me le strade possibili sono due:
- porre una distanza diversa tra ciascun mattone (se ci sono molti mattoni a sinistra e pochi, via via, a destra, è possibile far sporgere la fila anche si molto rispetto alla base senza far arrivare il baricentro oltre la superficie di appoggio)
-forzare il significato della parola sovrapporre e disporre i mattoni come un triangolo di tartaglia al contrario (così facendo però sono necessari davvero molti mattoni)
Ci penserò su, voi cosa ne pensate?
- porre una distanza diversa tra ciascun mattone (se ci sono molti mattoni a sinistra e pochi, via via, a destra, è possibile far sporgere la fila anche si molto rispetto alla base senza far arrivare il baricentro oltre la superficie di appoggio)
-forzare il significato della parola sovrapporre e disporre i mattoni come un triangolo di tartaglia al contrario (così facendo però sono necessari davvero molti mattoni)
Ci penserò su, voi cosa ne pensate?
Re: 124. Pila di mattoni
Allora non ho capito il testo perchè il CM degli N-1 deve cadere entro il perimetro di appoggio come la torre di Pisa. La sporgenza dovrebbe essere data dall'ascissa del mattone più sporgente e se è 1 km il CM degli N-1 deve cadere al di là del perimetro d'appoggio ovvero deve essere maggiore di 10. Se il testo dice altro allora... 

Re: 124. Pila di mattoni
@carol: al posto di impilarli partendo dal basso, prova a partire dall'alto (prima posizioni un mattone, poi quello sotto e così via) 
@ruben: la prima strada è giusta
@ruben: la prima strada è giusta
Re: 124. Pila di mattoni
Per caso con 20 mattoni l'estremitá destra della pila di mattoni sporge rispetto all'estremitá destra del mattone più in basso di circa 35.4 cm?
Re: 124. Pila di mattoni
Provo come dici ma non riesco a trovare una formula ricorsiva. Sono arrivato a 10 mattoni in funzione dell'ascissa del primo ma non trovo la formula ricorsiva che poi darebbe l'Nmo mattone. Continuerò... 

Re: 124. Pila di mattoni
Rispondo ora al primo quesito.
Numero i mattoni a partire da 1 dal basso verso l'alto.
Sia ora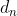 la distanza tra l'estremo sinistro del mattone n-esimo e l'estremo sinistro del mattone (n+1)-esimo.
la distanza tra l'estremo sinistro del mattone n-esimo e l'estremo sinistro del mattone (n+1)-esimo.
Avendo 20 mattoni, il mio n andrà da 1 a 19. Sia L la lunghezza di un mattone.
Noto subito (facendo un elementare disegno della situazione), che per calcolare la sporgenza massima del mattone più a destra rispetto a quello più in basso devo massimizzare la somma delle distanze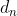 , che equivale alla sporgenza richiesta.
, che equivale alla sporgenza richiesta.
Ricordo ora la seguente "legge" fisica: quando impilo dei mattoni, la proiezione verticale del baricentro di tutto il sistema eccetto il mattone più in basso deve giacere all'interno o sul bordo del mattone più in basso. Per convincersene basta analizzare il sistema dato da due mattoni impilati: la distanza d in questo caso potrà essere pari al massimo a L/2.
Matematicamente questo si traduce nel seguente enunciato: quando analizzo i mattoni dal 20-esimo all'n-esimo, la media delle coordinate orizzontali dei centri di questi mattoni deve essere minore o uguale alla coordinata orizzontale dell'estremo destro del mattone (n-1)-esimo.
Noto subito (facendo un elementare disegno della situazione), che nel sistema di riferimento centrato sull'estremo sinistro del mattone (n-1)-esimo, tale condizione si esprime come+(d_{n-1}+d_n + \frac{L}{2}) + (d_{n-1}+d_n + d_{n+1} + \frac{L}{2}) + ... + (d_{n-1}+d_n + d_{n+1} + ... + d_{19} + \frac{L}{2}) = (20-n+1)L) , dove l'uguaglianza è data dalla necessità di massimizzare la somma di tutte le distanze, come richiesto dalla traccia.
, dove l'uguaglianza è data dalla necessità di massimizzare la somma di tutte le distanze, come richiesto dalla traccia.
Scrivendo tale condizione per il mattoni 20-esimo e per i mattoni dal 20-esimo al 19-esimo, dal 20-esimo al 18-esimo, e così via, arrivo al sistema lineare:
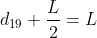
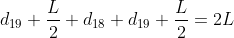
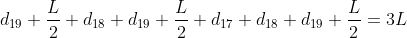
e così via...
Risolvendo il sistema partendo dall'equazione più in alto e andando man mano scendendo (per sostituzione) si trova:
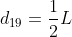 ,
, 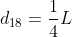 ,
, 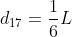 , e così via...
, e così via...
Allora}L) , da cui
, da cui 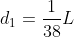 .
.
la sporgenza massima è allora L = 35.4 cm )
Numero i mattoni a partire da 1 dal basso verso l'alto.
Sia ora
Avendo 20 mattoni, il mio n andrà da 1 a 19. Sia L la lunghezza di un mattone.
Noto subito (facendo un elementare disegno della situazione), che per calcolare la sporgenza massima del mattone più a destra rispetto a quello più in basso devo massimizzare la somma delle distanze
Ricordo ora la seguente "legge" fisica: quando impilo dei mattoni, la proiezione verticale del baricentro di tutto il sistema eccetto il mattone più in basso deve giacere all'interno o sul bordo del mattone più in basso. Per convincersene basta analizzare il sistema dato da due mattoni impilati: la distanza d in questo caso potrà essere pari al massimo a L/2.
Matematicamente questo si traduce nel seguente enunciato: quando analizzo i mattoni dal 20-esimo all'n-esimo, la media delle coordinate orizzontali dei centri di questi mattoni deve essere minore o uguale alla coordinata orizzontale dell'estremo destro del mattone (n-1)-esimo.
Noto subito (facendo un elementare disegno della situazione), che nel sistema di riferimento centrato sull'estremo sinistro del mattone (n-1)-esimo, tale condizione si esprime come
Scrivendo tale condizione per il mattoni 20-esimo e per i mattoni dal 20-esimo al 19-esimo, dal 20-esimo al 18-esimo, e così via, arrivo al sistema lineare:
e così via...
Risolvendo il sistema partendo dall'equazione più in alto e andando man mano scendendo (per sostituzione) si trova:
Allora
la sporgenza massima è allora
