SGSS 2017-2 Asta che scivola
SGSS 2017-2 Asta che scivola
Un'asta di estremi A e B lunga  è posta verticalmente in modo che l'estremo B sia appoggiato al pavimento, mentre A sia a contatto con la parete. L'asta inizia a scivolare con velocità iniziale trascurabile in modo che B si muova a contatto con il pavimento. Trovare a che altezza e con velocità orizzontale del centro di massa il punto A perde il contatto con la parete.
è posta verticalmente in modo che l'estremo B sia appoggiato al pavimento, mentre A sia a contatto con la parete. L'asta inizia a scivolare con velocità iniziale trascurabile in modo che B si muova a contatto con il pavimento. Trovare a che altezza e con velocità orizzontale del centro di massa il punto A perde il contatto con la parete.
Re: SGSS 2017-2 Asta che scivola
Gli attriti sono trascurabili?
Re: SGSS 2017-2 Asta che scivola
Se non sbaglio, l'attrito non c'è ne' sulla parete ne' sul pavimento sennò non si muoverebbe. Inoltre sempre se non ho sbagliato i conti perchè ho preso forse una strada complicata a me risulterebbe che si stacca quando l'angolo con la verticale è 60° e quindi l'altezza è L/2. La velocità orizzontale del CM mi risulterebbe senza Latex  (3/4)L.radice di (g/L)
(3/4)L.radice di (g/L) 


Re: SGSS 2017-2 Asta che scivola
Immagino che per la velocità ci vada 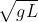 al posto di
al posto di 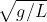 , perché altrimenti non torna dimensionalmente... comunque i risultati non mi tornano entrambi
, perché altrimenti non torna dimensionalmente... comunque i risultati non mi tornano entrambi 
Prova comunque a postare la strada che hai seguito
Prova comunque a postare la strada che hai seguito
Re: SGSS 2017-2 Asta che scivola
Credo che lui volesse scrivere 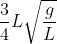 , che si trova dimensionalmente, e portando la
, che si trova dimensionalmente, e portando la  nella radice diventa quello che dici tu.
nella radice diventa quello che dici tu.
In ogni caso, qualche hint per farlo?
In ogni caso, qualche hint per farlo?
Re: SGSS 2017-2 Asta che scivola
Credo che la prima idea che convenga avere (e credo sia anche la meno standard) è sfruttare il fatto che il centro di massa dell'asta si muove su una circonferenza fintanto che i suoi estremi sono a contatto coi muri.
Re: SGSS 2017-2 Asta che scivola
Ops, avevo letto male e mi ero perso la L...
L'idea di Marcus è giusta e probabilmente anche la più veloce, alternativamente si può usare il procedimento più classico di scomporre il moto in una traslazione più una rotazione intorno al cdm
Re: SGSS 2017-2 Asta che scivola
Ho trovato le coordinate del baricentro in funzione dell'angolo formato con la verticale, poi ho derivato due volte ascissa e ordinata. Ho impostato le eq. della dinamica su x e y in funzione delle reazioni perp. alla parete e al piano e la rotazione attorno al baricentro con momento di inerzia e reazioni. Per il distacco ho imposto che si annullasse l'acc. CM rispetto a x ottenendo una relazione fra velocità angolare al quadrato e accelerazione angolare. Un'altra relazione fra queste l'ho trovata integrando con un trucco l'eq. della rotazione. Con queste ho trovato i risultati. Senza Latex dovete avere pazienza con i miei discorsi retorici poco chiari. 

Re: SGSS 2017-2 Asta che scivola
E' perchè, in un sistema di riferimento che ha per assi le pareti dei muri viste lateralmente, si ha per il teorema di Pitagora che
