Primo punto.
L'hint di Ippo di sfruttare l'analogia con il campo gravitazionale semplifica da un punto di vista fisico enormemente le cose. Infatti, come le particelle dell'aria sono soggette ognuna ad una stessa accelerazione, trascurando le variazioni di g per una distanza molto minore rispetto al raggio terrestre, allo stesso modo le particelle positive
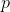
e negative

sono soggette ad una accelerazione costante infatti:
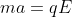
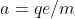 (1)
(1)
dove
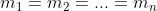
la massa delle particelle,
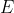
il campo elettrico costante e
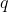
la carica di ogni particella
si noti che l'accelerazione è costante e uguale per ognuna poichè hanno la stessa masa e carica. Ovvio che metà delle particelle vanno da una parte e l'altra metà dall'altra.
A sto punto consideriamo l'energia totale riferito alle particelle cariche di un segno dentro il condensatore, quindi le particelle saranno N/2 di quel segno:
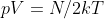 (2)
(2)
inoltre poichè
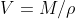
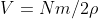
allora

dove
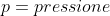
sconosciuta mentre
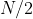
e

e
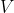
ci vengono fornite.
ora la legge di Stevino ci può essere utile per porre in relazione
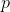
e
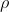
che vogliamo conoscre, allora si avrà:
=-\rho gx) (3)
(3)
ma invece di g poniamo la

trovata prima.
Dalla
)
si può ricavare come:
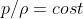
.
e quindi
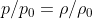 (4)
(4)
quindi ricordando che
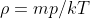
e che al posto di g ci va a
allora
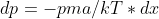
la riscriviamo meglio come

con
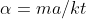
quindi integrando da
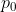
a
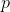
e da 0 a

si avrà:
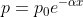
sostituendo
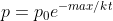
ed infine
-->
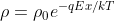
questa è la densità che hanno le particelle positive che partono dall'armatura negativa e dove la x=0. Mentre più ci si avvicina all'armatura positiva e più la densità delle particelle positive diminuisce, seguendo una funzione esponenziale.
Stessa storia vale anche per le particelle negative in modo simmetrico a quelle positive.
Spero di non avere sbagliato tutto!

Osservazione:
E' interessante notare come parlare di gravità o attrazione elettrica in questo caso è la stessa identica cosa. L'interazione infatti risulta del tipo
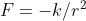
. Questo fatto non è da sottovalutare poichè è questa condizione che stà alla base della legge di Stevino posta in quel fantastico modo.
[Edit] Secondo punto.
Dato che la densità è una grandezza intensiva allora non si può sommare semplicemente la densità di due sostanze. Per poter bypassare tale ostacolo consideriamo semplicemente che il volume in cui conteremo le particelle postive e negative sarà uguale al volume nel quale si conterebbero singolarmente le cariche negative e quelle positive rispettivamente, quindi avremmo a che fare con le masse o con il numero delle particelle, che sono una grandezza sommabile normalmente.
Supposto ciò
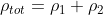
calcolate nello stesso volume
quindi si avrà:
})
dove x=0 è fissato nell'armatura a sinistra considerata negativa per comodità.
ora
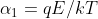
e
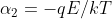
e quindi
})
}e^{-2d})
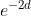
è una costante
allora per le eguaglianze postate da Ippo si ha:
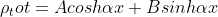
Punto terzo.
Se e solo se il punto uno è giusto

, in sostanza si esegue lo stesso procedimento...
La fisica è come il sesso: certamente può fornire alcuni risultati pratici, ma non è questo il motivo per cui lo facciamo!
-Richard Feynman
