Al solito posto il procedimento se i risultati sono corretti. Il distacco avviene se la reazione della parete, che deve essere positiva cioè rivolta verso il centro come la forza centripeta, si annulla. E' allora opportuno, considerando l'angolo

con vertice nel centro della circonferenza sezione formato con la verticale dal raggio posizione dell'oggetto, considerare prima il caso

e poi

. Ho trovato nei due casi
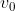
per cui si distacca dalla parete in funzione di
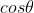
e sostituendo i valori numerici per

mi risulta
1)
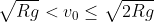
nel primo caso e
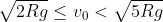
nel secondo per cui insomma
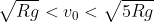
2) per l'altezza a cui avviene il distacco dalla parete mi risulta
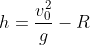
nel primo caso che si raccorda a 90° con
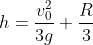
trovata nel secondo caso. (Infatti per
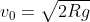
risulta in entrambe h=R come deve essere a 90°)
3) la quota altezza massima della traiettoria la raggiunge per v=0 ed è
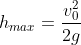
. Infatti se v=0 tutta l'energia cinetica iniziale si trasforma in energia potenziale e quindi in quota. Nel caso però che
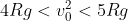
pur avvenendo il distacco prima di 2R come chiede 1), il massimo è superiore a 2R per cui la traiettoria parabolica concava verso il basso che si libera dalla parete, incontra il cilindro in prossimità di 2R e viene respinta verso il basso.
Tutto ciò ovviamente se non ho sbagliato il procedimento e/o i conti. Sono ormai giorni che ci penso...


