Pigkappa ha scritto: ↑11 feb 2018, 22:28
Assumi che
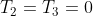
per cominciare. Se
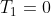
, e' intuitivo che
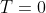
ovunque. Se
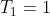
(1 grado, o 1 in qualsiasi unita' vuoi), la soluzione sara' data da una qualche funzione che chiamo
)
e non conosciamo.
Le equazioni di propagazione del calore, e specialmente l'equazione che deve soddisfare
)
sono lineari. Chi fa il liceo queste equazioni non le conosce perche' sono complicate, ma per risolvere il problema bisogna fidarsi del fatto che sono lineari. Se sono lineari, moltiplicare le condizioni al bordo per una costante fa si' che anche la soluzione sia moltiplicata per la stessa costante. Per cui se invece di
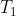
la temperatura nel primo vertice e'
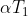
, la temperatura sara'
)
.
Se invece che
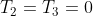
si ha
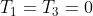
e
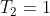
, la temperatura in ogni punto sara' data da una funzione
)
.
)
non e' uguale a
)
perche' i vertici sono due vertici diversi. Presumibilmente se ruoti
)
di 120 gradi intorno al centro del triangolo troverai
)
. E' comunque chiaro che nel centro del triangolo,
 = T_1(x,y))
, e similarmente se definisci
)
anche quella sara' uguale.
Se
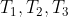
sono uguali a
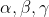
, a questo punto dovresti riuscire a convincerti che
 = \alpha T_1(x,y) + \beta T_2(x,y) + \gamma T_3(x,y))
. Inoltre nel centro del triangolo le tre funzioni sono uguali, per cui
 = (\alpha + \beta + \gamma) * T_1(\text{centro}).)
Se
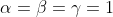
, intuiamo che la temperatura sara' 1 ovunque, da cui
 * T_1(\text{centro}))
, da cui
 = 1/3)
e nel caso generale la temperatura e'
 = (\alpha + \beta + \gamma) / 3)
.
Per chi conosce le derivate parziali, l'equazione di propagazione del calore e' nella forma
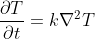
. All'equilibrio
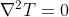
. BeppeBogna si riferiva all'equazione del potenziale elettrico che in generale e'
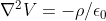
; nel vuoto (carica
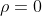
) diventa
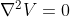
.
per cominciare. Se
, e' intuitivo che
ovunque. Se
(1 grado, o 1 in qualsiasi unita' vuoi), la soluzione sara' data da una qualche funzione che chiamo
e non conosciamo.
sono lineari. Chi fa il liceo queste equazioni non le conosce perche' sono complicate, ma per risolvere il problema bisogna fidarsi del fatto che sono lineari. Se sono lineari, moltiplicare le condizioni al bordo per una costante fa si' che anche la soluzione sia moltiplicata per la stessa costante. Per cui se invece di
la temperatura nel primo vertice e'
, la temperatura sara'
.
si ha
e
, la temperatura in ogni punto sara' data da una funzione
.
non e' uguale a
perche' i vertici sono due vertici diversi. Presumibilmente se ruoti
di 120 gradi intorno al centro del triangolo troverai
. E' comunque chiaro che nel centro del triangolo,
, e similarmente se definisci
anche quella sara' uguale.
sono uguali a
, a questo punto dovresti riuscire a convincerti che
. Inoltre nel centro del triangolo le tre funzioni sono uguali, per cui
, intuiamo che la temperatura sara' 1 ovunque, da cui
, da cui
e nel caso generale la temperatura e'
.
. All'equilibrio
. BeppeBogna si riferiva all'equazione del potenziale elettrico che in generale e'
; nel vuoto (carica
) diventa
.
