Si abbiano n corpi, considerabili come puntiformi, fermi in vari punti dell’asse x, sul
quale possono scorrere liberamente. Le rispettive masse siano m1, ….., mn dove l’indice è
ordinato in modo crescente secondo l’ascissa dei rispettivi corpi.
Il corpo numero 1 viene poi lanciato con velocità positiva lungo l’asse x. Ne consegue
una serie di urti, tutti elastici, tra le varie masse finchè viene messo in moto l’n-esimo
corpo, con velocità Vn. Siano fissati i valori di tutte le masse, tranne la i-esima, con
1<i<n. Quanto deve valere mi perchè Vn abbia il valore massimo possibile?
Urti elastici
Re: Urti elastici
Siccome non ti ha ancora risposto desidero "espormi" anch'io. Anche a me tornava così perchè ho pensato che contavano solo tre punti materiali... 

Re: Urti elastici
Se torna anche a carol... posto la mia soluzione 
si ha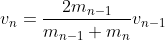 da cui
da cui
(m_2+m_3)...(m_{n-1}+m_n)})
tralasciando le costanti abbiamo da massimizzare = \frac{m_i}{(m_i+m_{i+1})(m_i+m_{i-1})}) . Ponendo la sua derivata uguale a 0 otteniamo
. Ponendo la sua derivata uguale a 0 otteniamo 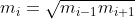

si ha
tralasciando le costanti abbiamo da massimizzare
Re: Urti elastici
Si credo di aver capito che usi quella formula ricorsiva che deriva dalla conservazione dell qdm e dell'energia. 

Io invece approfittando del fatto che i deve essere maggiore di 1 e minore di n, l'ho preso uguale ad n-1 disinteressandomi dei precedenti. Applicando le conservazioni ho massimizzato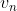 ottenendo il risultato tuo
ottenendo il risultato tuo 

Io invece approfittando del fatto che i deve essere maggiore di 1 e minore di n, l'ho preso uguale ad n-1 disinteressandomi dei precedenti. Applicando le conservazioni ho massimizzato
Re: Urti elastici
Che succede se prendiamo le masse degli indici pari uguali alla media geometrica di quelle a indici dispari precedenti e seguenti? 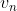 diventa il massimo dei massimi o che cosa?
diventa il massimo dei massimi o che cosa? 


